Division Algebras And Quantum Theory

03 Jun, 2021

During the past decade Frobenius algebras have shown up in a variety of topological contexts in theoretical physics and in computer science. Indeed these three choices appear naturally in a number of axiomatic approaches.

Quantum Mechanics I Have No Idea What This Means Theoretical Physics Quantum Mechanics Physics Quantum Physics

With all this extra structure Ktheory becomes a powerful tool in some ways more powerful even than ordinary cohomology.

Division algebras and quantum theory. Quantum theory may be formulated using Hilbert spaces over any of the three associative normed division algebras. Figueroa-OFarrill 1 Department of Physics Queen Mary and Westfield College Mile End Road London El 4NS UK Received 10 June 1998. So mathematically at least there are three possible kinds of quantum mechanics.

We have recently proposed a Lagrangian in trace dynamics at the Planck scale for unification of gravitation Yang-Mills fields and fermions. Indeed these three choices appear naturally in a number of axiomatic approaches. PDF This is a review of Division algebras and quantum theory.

We follow the streamlined discussion in Baez-Huerta 09 and Baez-Huerta 10. It is known that the octonions and the fact that only four normed division algebras can exist relates to the spacetime dimensions in which supersymmetric quantum field theories can be constructed. However there are internal problems with real or quaternionic quantum theory.

The relation between real spin representations and division algebras is originally due to Kugo-Townsend 82 Sudbery 84 and others. The Racah-Wigner Algebra in Quantum Theory. Received in revised form 15 April 1999 Abstract We present a novel.

The prime example of this is the very simple proof once the basic machinery of complex Ktheory has been set up of the theorem that there are no ﬁnite dimensional division algebras over Rin dimensions. The real numbers the complex numbers and the quaternions. But one thing the Division Algebras and Supersymmetry series has to offer is a focus on the way normed division algebras help create the exceptional higher algebraic structures that underlie superstring and super-2-brane theories.

Find read and cite all the research you need on ResearchGate. Quantum theory may be formulated using Hilbert spaces over any of the three associative normed division algebras. Quantum theory may be formulated using Hilbert spaces over any of the three associative normed division algebras.

Quantum theory may be formulated using Hilbert spaces over any of the three associative normed division algebras. Search within full text. And as youre undoubtedly sick of hearing there are three choices.

Composites and Categories of Euclidean Jordan Algebras. 17 18 Also attempts have been made to obtain the Standard Model of elementary particle physics from octonionic constructions for example. Indeed these three choices appear naturally in a number of axiomatic approaches.

The real numbers the complex numbers and the quaternions. Howard Barnum 123 Matthew A. The real numbers the complex numbers and the quaternions.

The Racah-Wigner Algebra in Quantum Theory. At energies much lower than Planck scale trace dynamics reduces to quantum field theory. The Racah-Wigner Algebra in Quantum Theory.

You can set up a theory of Hilbert spaces based on any normed division algebra. And with the completion of this series I can now relax and forget all about these ideas confident that at. In physics the main scenery for Frobenius algebras is that of topological quantum eld.

SICs are of importance to quantum foundations and in particular to the research program of approaching quantum foundations by way of quantum information theory 141516A SIC defines a mapping from quantum states to probability distributions and because this mapping is informationally complete any calculation that can be done given a quantum. However there are internal problems with real or quaternionic quantum theory. JOURNAL OF GEOM D PHYSICS ELSEVIER Journal of Geometry and Physics 32 1999 227-240 Gauge theory and the division algebras JosM.

In algebra and representation theory such algebras have been studied for a century. However there are internal problems with real or quaternionic quantum theory. Evolution takes place in Connes time.

The real numbers ℝ mathbbR the complex numbers ℂ mathbbC and the quaternions ℍ mathbbH. Dynamical variables are described by odd-grade fermionic and even-grade bosonic Grassmann matrices. The real numbers the complex numbers and the quaternions.

However there are internal problems with real or quaternionic quantum theory. Indeed these three choices appear naturally in a number of axiomatic approaches. The real numbers the complex numbers and the quaternions.

Log in Register Recommend to librarian. Quantum theory may be formulated using Hilbert spaces over any of the three associative normed division algebras. For instance quantum field theory in dimension 01 is the worldline theory of particles also known as quantum mechanics.

Graydon 45 and Alexander Wilce 6. Buy the print book Check if you have access via personal or institutional login.

Quantum Mechanics Theory And Applications Fundamental Theories Of Physics 137 Ghatak Ajoy Lokanathan S 9781402018503 Amazon Com Books

Max Plank S Quantum Theory For 11th Class Chemistry Planck S Quantum Theory Quantum Chemistry

Quantum Flashes Could Be What Finally Links Relativity And Quantum Theory Sciencealert Quantum Relatable Quantum Computer

0807 0060 Gauge Gravity And Electroweak Theory Theory Of Gravity Theories General Relativity

Quantum Theory Of Light Steemit Quantum Physics Physics Mechanics Physics

Quantum Theory

Andy S Quantum Mechanics I P 1 Physics Teaching Ideas Physics Answers Physics

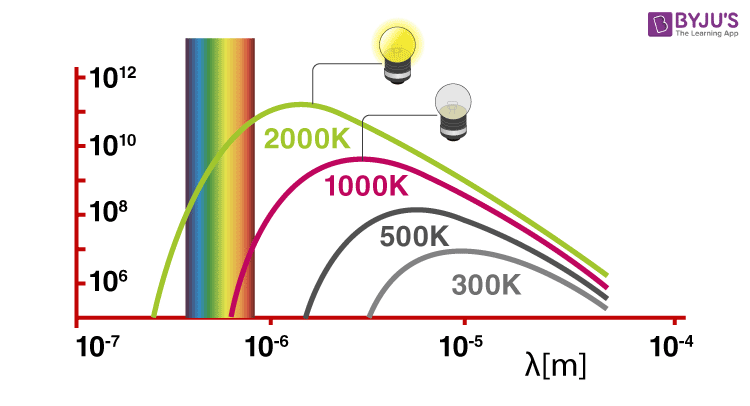
Planck S Quantum Theory Black Body Radiation Planck S Constant Byju S

New Experiment Explores The Origin Of Probabilities In Quantum Physics Quantum Physics Physics Quantum

5 Math Equations That Change The Way You See The World Equations Teaching Algebra Mathematics

Mathematics Of Classical And Quantum Physics Dover Books On Physics Revised Ed Byron Frederick W Fuller Robert W Amazon Com

Physics Ch 66 Ch 4 Quantum Mechanics Schrodinger Eqn 53 Of 92 The Wave Equation Youtube

Pin By George M On Science Math Methods Mathematics Math Vocabulary

Taken From Klee Irwin S Blog 3d Printer Challenge Can You Print The Qsn Kleeirwin Kleeirwinblog Blog Deepthought Theoretical Physics Print 3d Printing